A processes synchronize problem from my OS lecture…

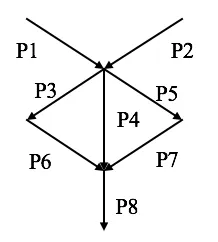
(Using Semaphore primitive to write pseudo code, make it right and concurrency.) There are processes and their execution order must satisfy the following DAG. For example, P3 must be executed after P1 and P2, while P6 must wait for P3.

My Simple Solution

For each process,

M := the mutex indicate that process is ready to execute
NODE := the node that this process point to

For each node,

MUTEX := mutex access this node
CNT := the number of processes that have reach this node, initial 0.
N := in-degree of the node
OUT := the set of all out edges

And the pseudo code of each process is:

Process(P) {
  Wait(P.M) // wait for this process is ready to execute

  // ...

  Wait(P.NODE.MUTEX) // mutex access the node it point to
    P.NODE.CNT += 1
    if P.NODE.CNT == P.NODE.N:
      for each process E in P.NODE.OUT:
        Signal(E.M)
  Signal(P.NODE.MUTEX)
}

The complete solution of the problem (simplify the processes that do not wait for others and the node where both in-degree and out-degree is 1):

S3 = Semaphore(0)
S4 = Semaphore(0)
S5 = Semaphore(0)
S6 = Semaphore(0)
S7 = Semaphore(0)
S8 = Semaphore(0)

M1 = Semaphore(1)
cnt1 = 0
N1 = 2

M2 = Semaphore(1)
cnt2 = 0
N2 = 3

P1() {
  // ...
  P(M1)
    cnt1++
    if cnt1 == N1: V(S3), V(S4), V(S5)
  V(M1)
}

P2() {
  // ...
  P(M1)
    cnt1++
    if cnt1 == N1: V(S3), V(S4), V(S5)
  V(M1)
}

P3() {
  P(S3)
  // ...
  V(S6)
}

P4() {
  P(S4)
  // ...
  P(M2)
    cnt2++
    if cnt2 == N2: V(S8)
  V(M2)
}

P5() {
  P(S5)
  // ...
  V(S7)
}

P6() {
  P(S6)
  // ...
  P(M2)
    cnt2++
    if cnt2 == N2: V(S8)
  V(M2)
}

P7() {
  P(S7)
  // ...
  P(M2)
   cnt2++
   if cnt2 == N2: V(S8)
  V(M2)
}

P8() {
  P(S8)
  // ...
}

Barrier Pattern

In The Little Book of Semaphores, there is a data struct called Barrier, works for the pattern that each process cannot pass through the critical point until all processes have reached that point.

A simplified C version of barrier:

struct {
  int n, cnt;
  sem_t mutex, barrier;
} barrier_t;

// n is the number of processes
void init_barrier(barrier_t *b, int n) {
  b->n = n;
  b->cnt = 0;
  init_sem(&b->mutex, 1);
  init_sem(&b->barrier, 0);
}

void go_through_barrier(barrier_t *b) {
  P(&b->mutex);
    b->cnt++;
    if (b->cnt == b->n)
      V(&b->barrier);
  V(&b->mutex);

  P(&b->barrier);
  V(&b->barrier);
}

We can find the common pattern of barrier and the DAG in the beginning: wait for a semaphore to reach a given number (n in the barrier pattern and in-degree of the node in the DAG). Therefore we can create a new type of synchronization primitive for this pattern:

struct {
  int n, cnt;
  sem_t mutex;
} n_sem_t;

void init_n_sem(n_sem_t *sem, int n) {
  sem->n = n;
  sem->cnt = 0;
  init_sem(&sem->mutex, 1);
}

void wait_n_sem(n_sem_t *sem) {
  while (sem->n != sem->cnt) ;
}

void post_n_sem(n_sem_t *sem) {
  wait(&sem->mutex);
  sem->cnt++;
  post(&sem->mutex);
}

The problem at the beginning can be solved using this primitive:

n_sem_t node1;
init_n_sem(&node1, 2);

void P1() {
  // ...
  post_n_sem(&node1);
}

void P3() {
  wait_n_sem(&node1);
  // ...
  // post next n_sem
}

A Processes Synchronize Problem and Barrier Pattern

My Simple Solution

Barrier Pattern